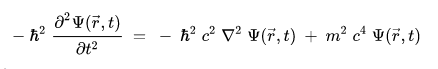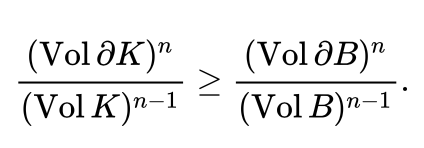Théorème isopérimétrique
En mathématiques, et plus précisément en géométrie, un
théorème isopérimétrique est une généralisation des résultats plus élémentaires d'isopérimétrie montrant par exemple que le disque est, à périmètre donné, la figure ayant la plus grande aire. Les questions traitées par cette généralisation concernent les compacts d'un espace métrique muni d'une mesure. Un exemple simple est donné par les compacts d'un plan euclidien. Les compacts concernés sont ceux de mesures finies ayant une frontière aussi de mesure finie. Dans l'exemple choisi, les compacts concernés sont ceux dont la frontière est une courbe rectifiable, c'est-à-dire essentiellement non fractale. Les mesures du compact et de sa frontière sont naturellement différentes : dans l'exemple, la mesure du compact est une aire, tandis que celle de sa courbe frontière est une longueur.
Un théorème isopérimétrique caractérise les compacts ayant la mesure la plus grande possible pour une mesure de leur frontière fixée. Dans le plan euclidien en utilisant la mesure de Lebesgue, un théorème isopérimétrique indique qu'un tel compact est un disque. En dimension 3, toujours avec une géométrie euclidienne, une autre version du théorème indique que c'est une boule. D'une manière plus générale, dans un espace euclidien de dimension
n, muni de la mesure de Lebesgue, l'optimum est obtenu par une boule, ce qui donne l'inégalité isopérimétrique suivante, si
K est un compact et
B la boule unité :
Les théorèmes isopérimétriques sont souvent difficiles à établir. Même un cas simple, comme celui du plan euclidien muni de la mesure de Lebesgue, est relativement technique à démontrer. Une des méthodes de preuve, connue depuis la démonstration de Hurwitz en 1901, est d'utiliser un résultat d'analyse issu de la théorie des séries de Fourier : l'inégalité de Wirtinger. Le résultat reste partiel car il ne traite que des surfaces dont la frontière est une courbe de classe C1.